

원이 빙글빙글 도는 것은
보고만 있어도 즐겁죠!
[Math] 삼각함수로 원 그리기!
안녕하세요! 밤말팅입니다~ 최근 삼각함수를 사용해서 원을 그릴 일이 조금 있었는데요! 아무래도 함수만 가지고는 잘 와닿지 않는 부분이라서 헷갈려하시는 분들이 조금! 있으신 것 같아서ㅎ
game-part-factory.tistory.com
저번 시간에 저희는 삼각함수로
원을 그리는 데에 성공했습니다!
Cos과 Sin만으로 이뤄낸 성과죠!
오늘은 여기서 한 단계
더 나아갑니다!
이번엔
구
로 가봅시다!

위에서 보여드렸던 그림을
살짝 뉘여놓은 그림입니다!
그리고 축을 하나 더 늘렸어요!
드디어 저희는 3차원으로 이동합니다!
원을 그릴 때처럼
"각도"를 이용해서 그릴 건데요!
| 각도 | 방향 |
| 90도 | 위 |
| 0도 | 앞 |
| -90도 | 아래 |
이런 느낌으로 잡아봅시다!
그렇지만 사실
3D로 넘어왔다고 해서
원을 그리는 데에
다른 걸 사용하진 않습니다!
여전히 Sin과 Cos으로
그리기를 할 거에요!

이제 저희가 원래 사용하던 Sin을
그대로 이용해서
축만 위 아래로 맞췄어요!
별 다른 점은 없습니다!
그렇다면 이걸 적용하면
어떤 모양이 될까요?
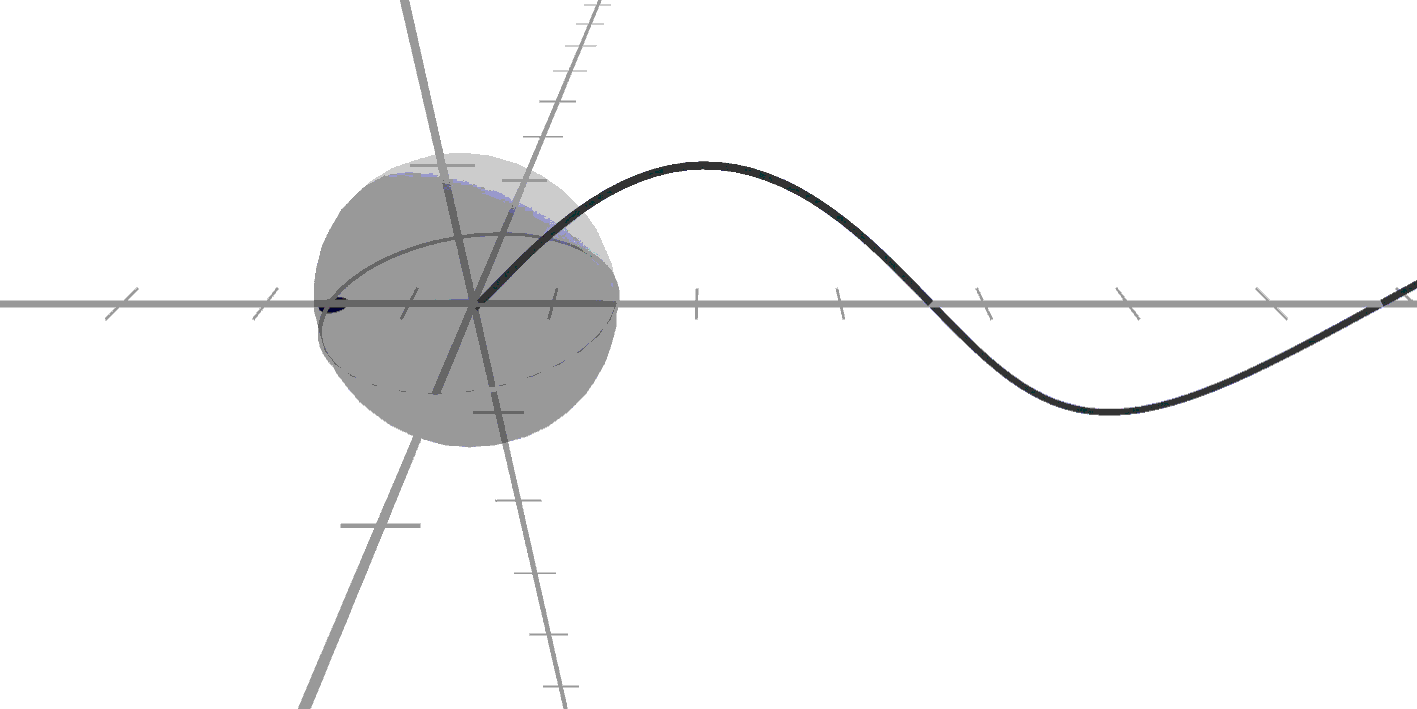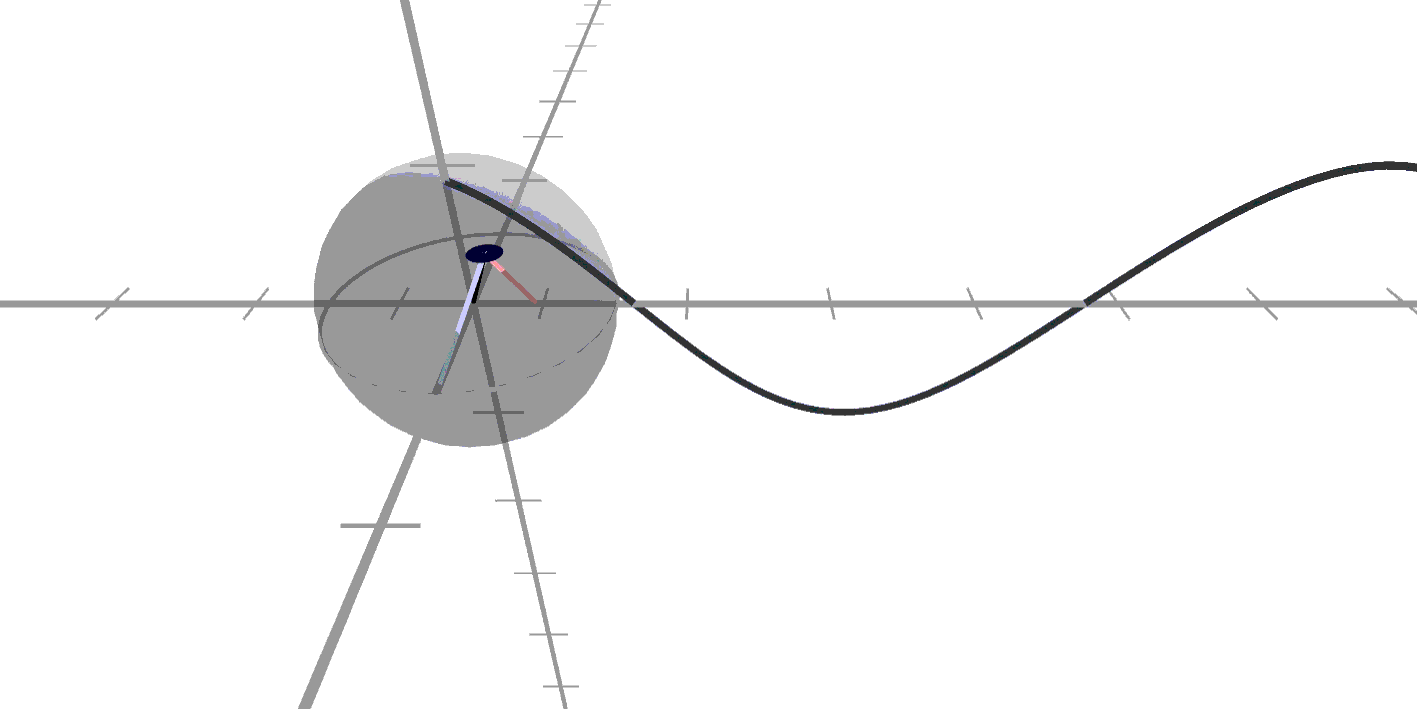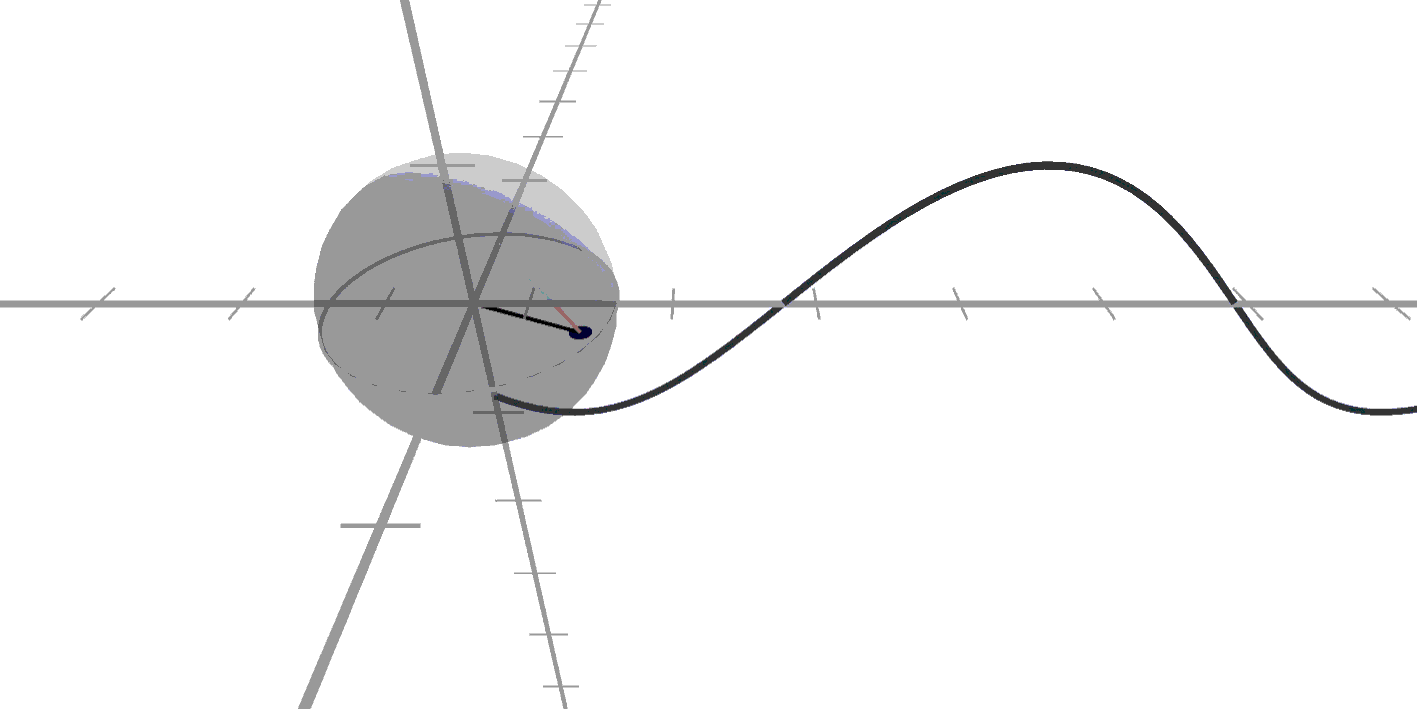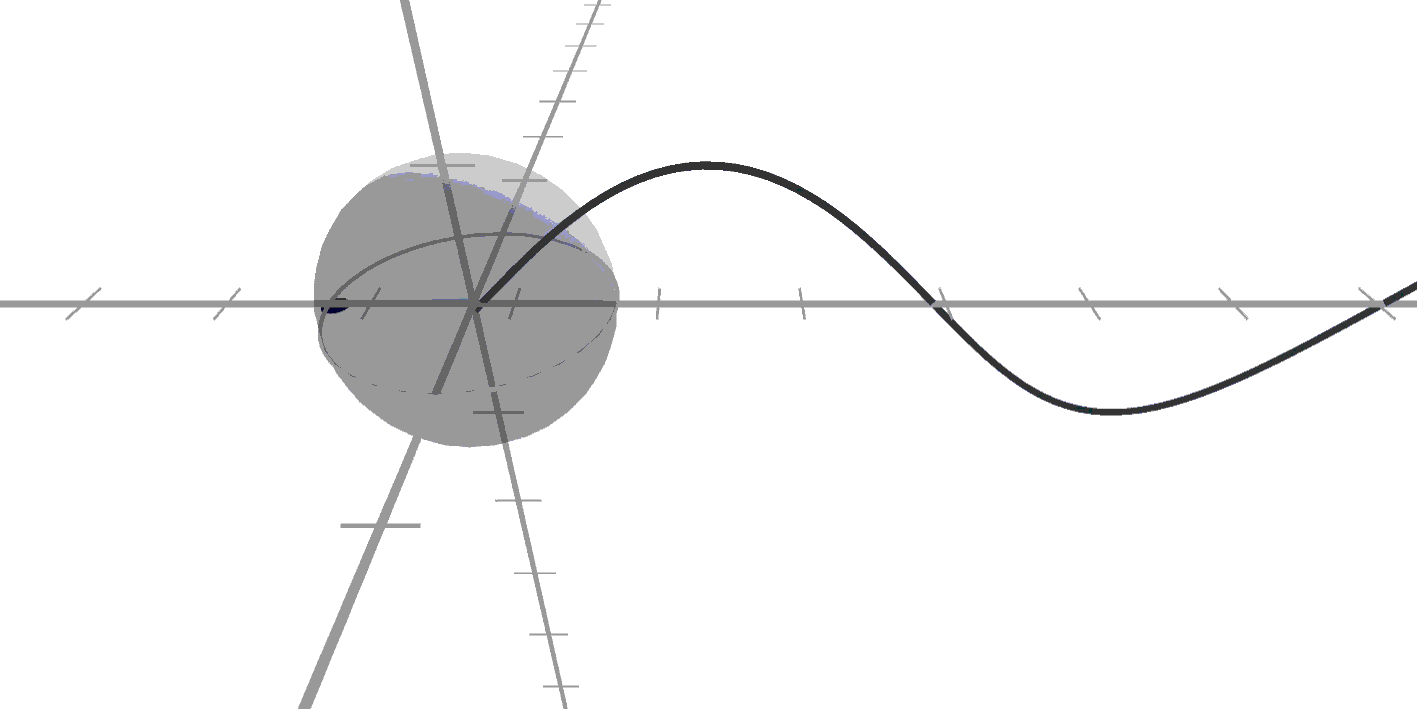
뭔가 이상한 느낌이죠?
맘대로 늘어나고 줄어드는 것
같아보이기도 하고..
대각선으로만 도네요!
위에서도 한 번 보죠!
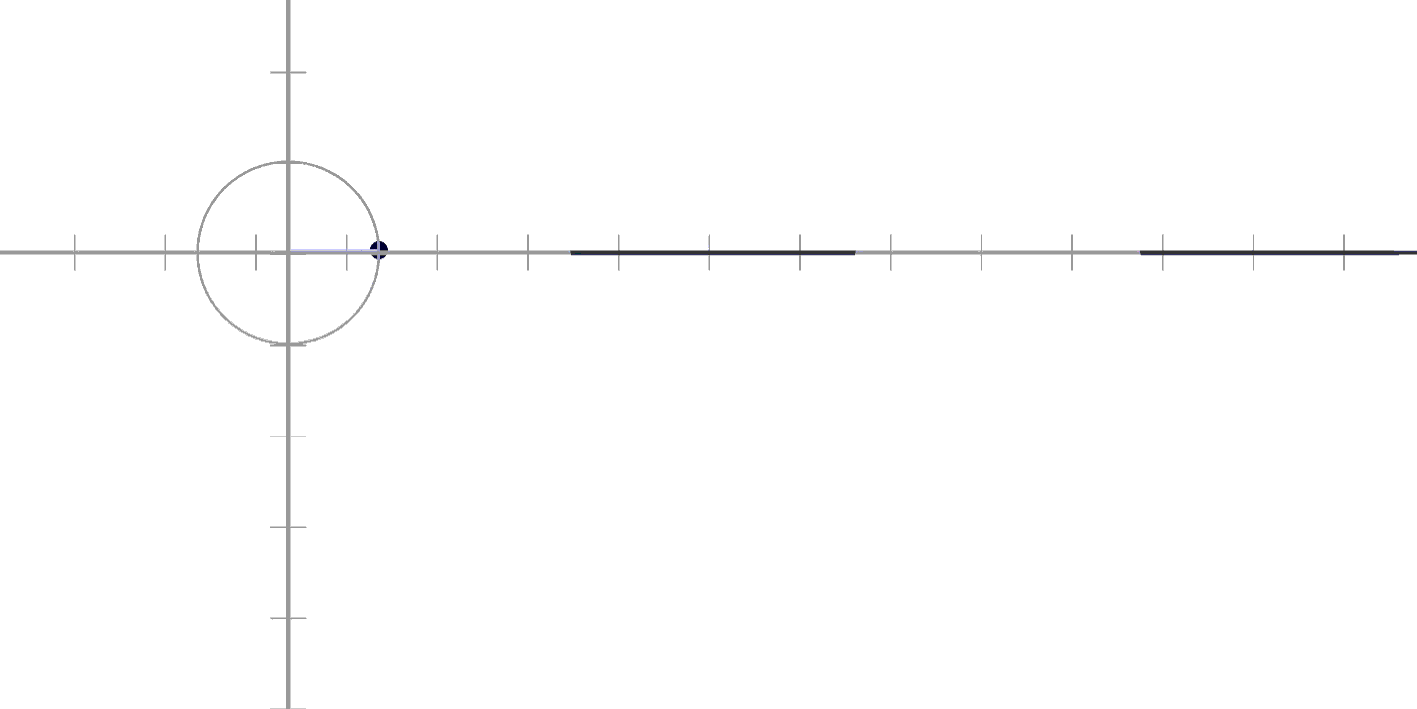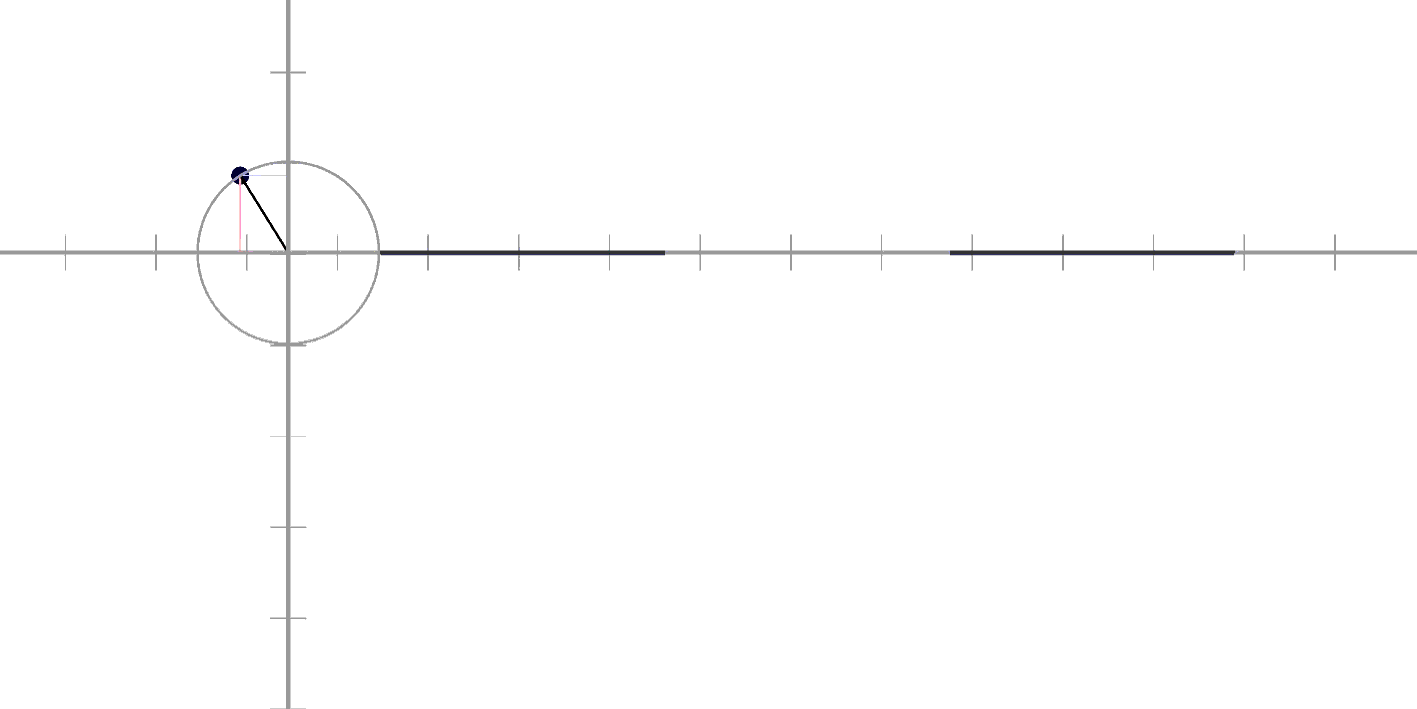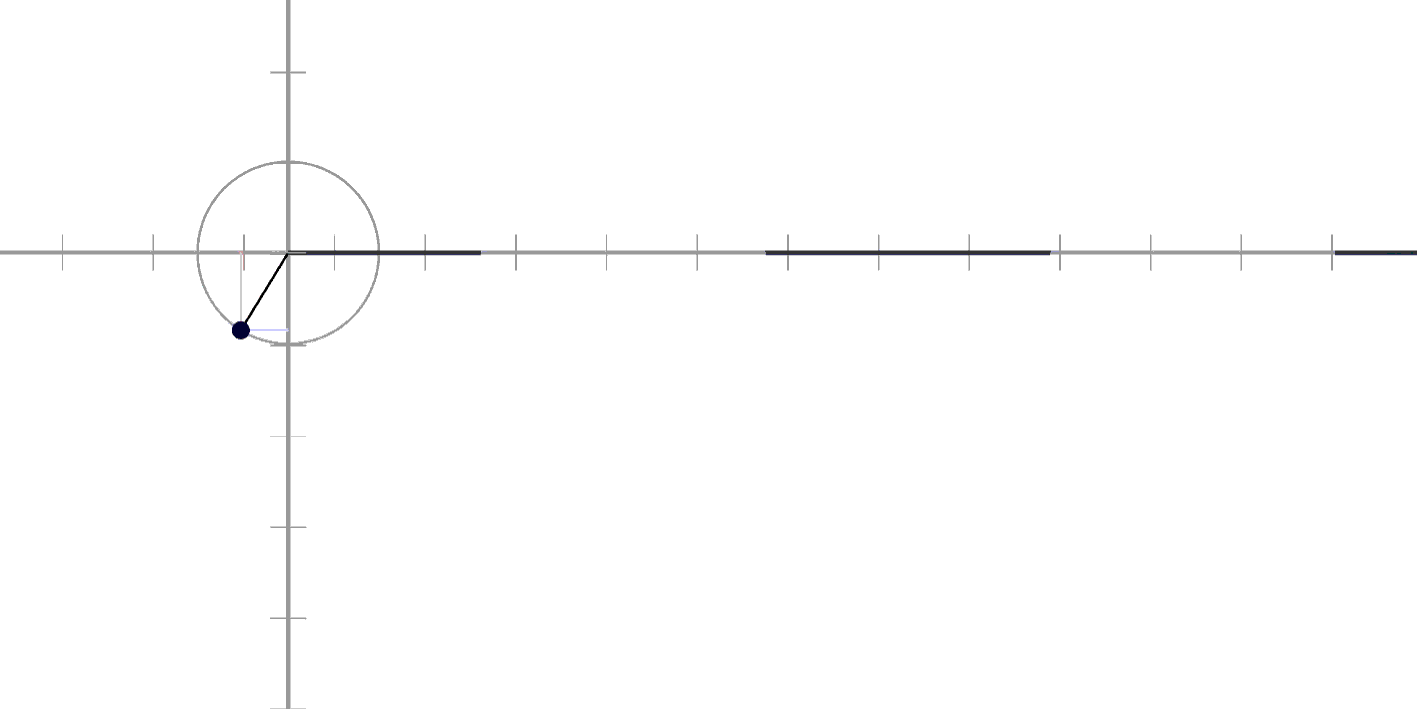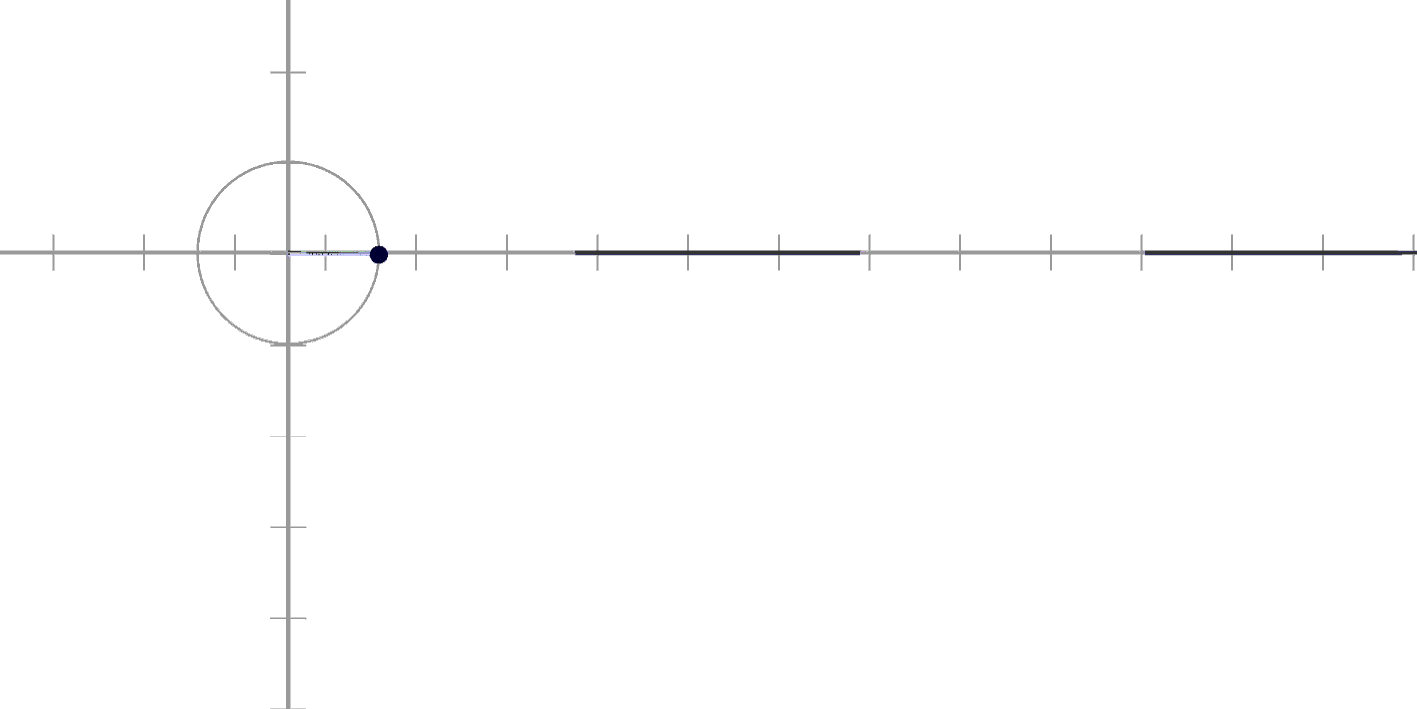
위에서 보면 이런 느낌입니다!
검은 선이 지금 Sin이에요!
오르내리고 있어서
수직선에 가리거나 보이거나 하죠?
그런데.. 위에서 볼 때에는
아까랑 변화가 없네요!
정확히 지금은 이런 모양으로
움직이는 중입니다!

위 아래로 같이 움직이지만
문제는 위로 갈수록
구는 줄어들어야 하는데
줄어드는 부분이 없으니
원통처럼 움직이는 것이죠!
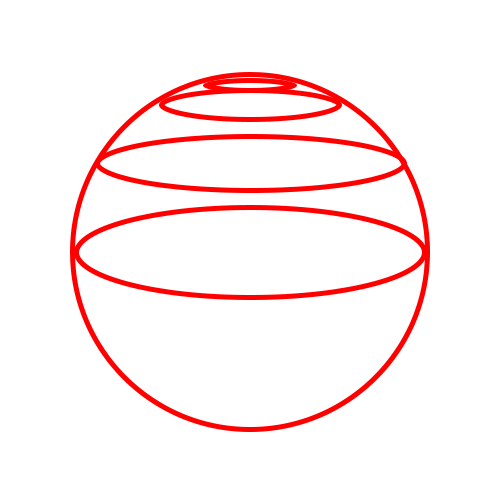
그래서 저희는
수직 각도가 더 클 수록
원의 크기 자체를
줄여야 합니다!
다행히 이걸 위한
함수가 아직 남아있죠!
바로 수직 Cos입니다!
지금까지는 위아래로 Sin만
적용을 했었죠?
적용한 현재 상태는
이렇습니다!
표시할 때 z를 높이라고 할게요!
x = Cos(수평각도)
y = Sin(수평각도)
z = Sin(수직각도)
라는 상태죠!
음.. 축 세 개를 모두 사용했는데
Cos(수직각도)는 어디에 넣어야할까요?
저희가 원의 크기를 줄이려고
생각했기 때문에

작아지는 양을 Cos으로
계산해볼 수 있습니다!
그래서 수평에서 계산했던 원을
Cos의 크기대로 줄이기만
끝이에요!
대신 이제 코사인은
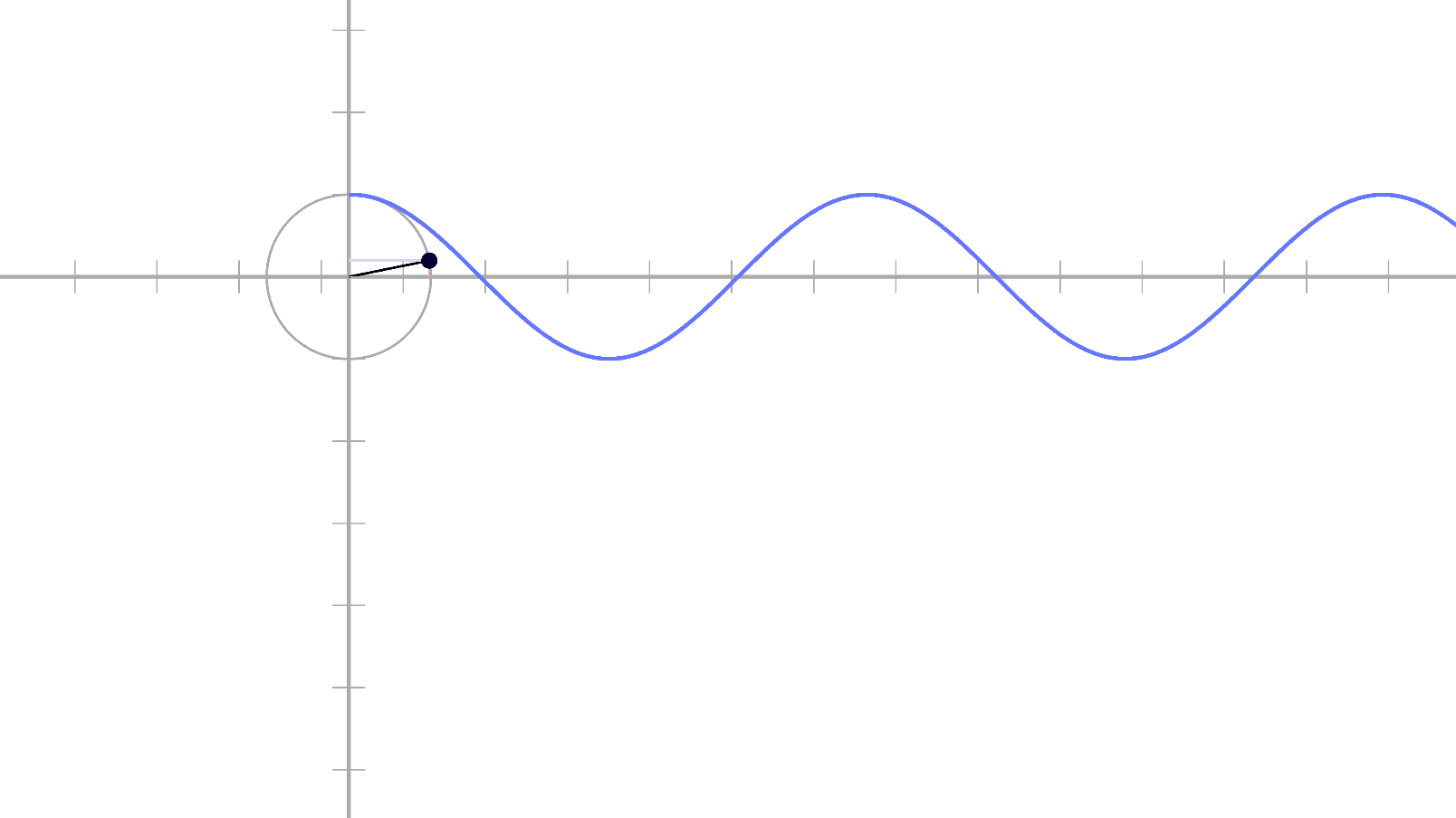
음수로도 갈 수 있어서
절대값(Abs)으로 적용해줄게요!
여기선 크기가 음수일 수는
없으니까요!
x = Cos(수평각도) * Abs(Cos(수직각도))
y = Sin(수평각도) * Abs(Cos(수직각도))
z = Sin(수직각도)
위에서 그냥 Abs(Cos(수직각도))만 곱한 거죠!
그러면

이런 형태가 됩니다!
음.. 아직 잘 모르겠네요!
지금은 수평각도와 수직각도가
같은 속도로 움직이고 있어서
모양이 맘에 안드는데요!
직접 따로 돌리면
이런 모양입니다!
어떤가요?
직접 조종을 해보니 조금 더
그럴싸한 것 같네요!
결국 Sin과 Cos을 응용해서
원하는 방향을 가리키는
벡터 하나를 얻을 수 있었군요!
단지 3차원이라서
어디에다가 적용해야되는지
위치만 바뀌었을 뿐인 것 같네요!
자 그래서 간단하게
구를 마쳐보았습니다!
혹시나 여기에서 더 궁금하신 점!
있으시면 남겨주시구요!
저는 그럼 또 다음 언젠가
다시뵙겠습니다~
읽어주셔서 감사합니다!!
'부품 설명서' 카테고리의 다른 글
| [Math] 삼각함수로 원 그리기! (0) | 2022.06.22 |
|---|---|
| [C#][C++] 콤보 시스템으로 배우는 Trie 만들기 (2) | 2021.05.21 |
| [C#][C++] 넣고, 뽑으면 끝나는 랜덤박스 만들기! (0) | 2021.05.17 |
| [C#] 문자열로 조작 가능! 대화창 만들기! (0) | 2021.01.30 |
| [C#] 은는이가 타파!! 자연스러운 문장 만들기! (0) | 2021.01.19 |