[Math] 삼각함수로 원 그리기!
안녕하세요! 밤말팅입니다~
최근 삼각함수를 사용해서 원을 그릴 일이
조금 있었는데요!
아무래도 함수만 가지고는
잘 와닿지 않는 부분이라서
헷갈려하시는 분들이 조금!
있으신 것 같아서ㅎㅎ
그림이랑 같이 들어갑니다!
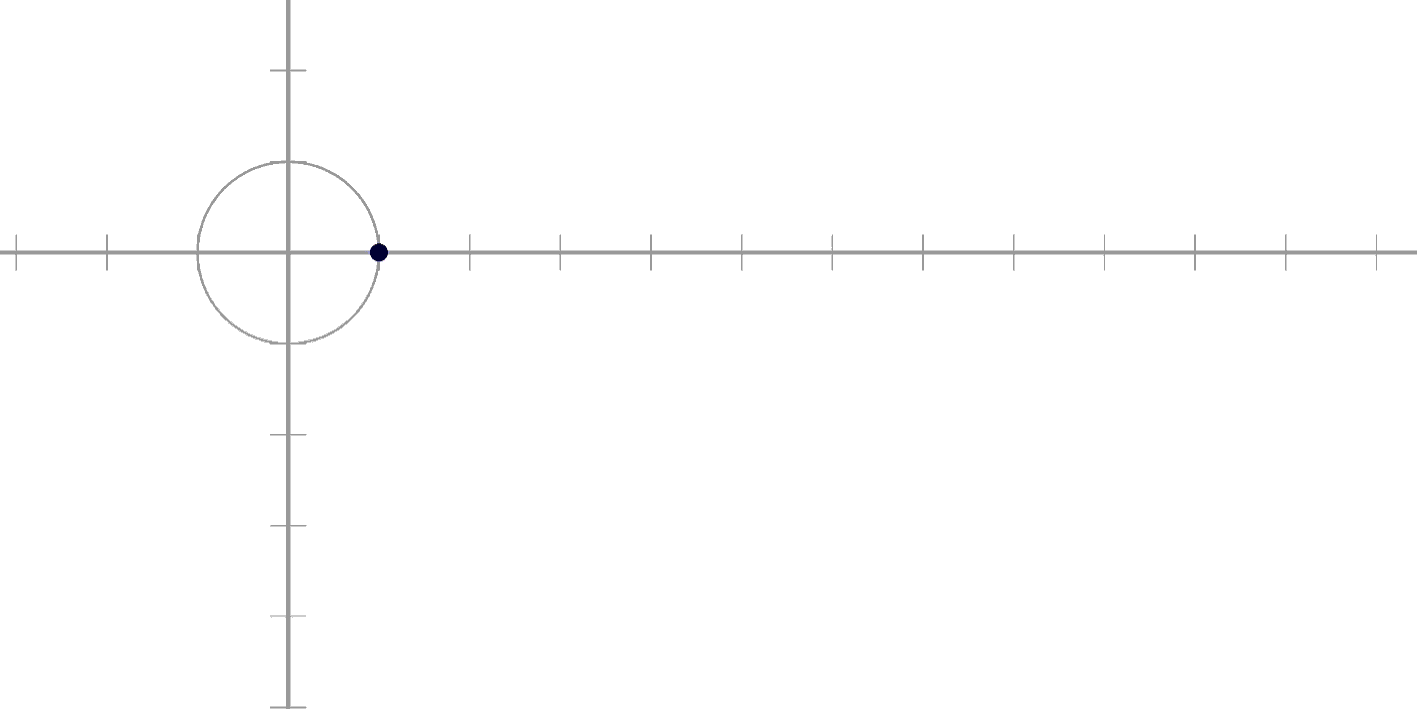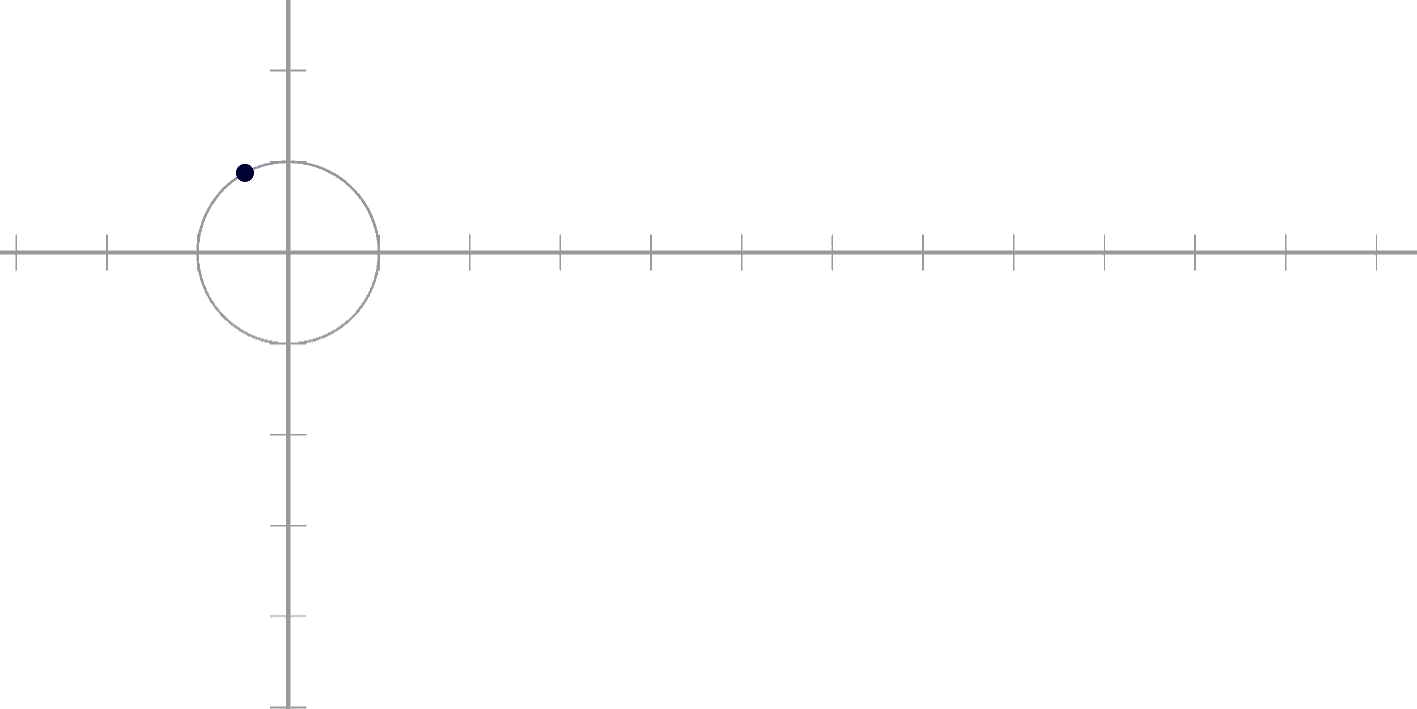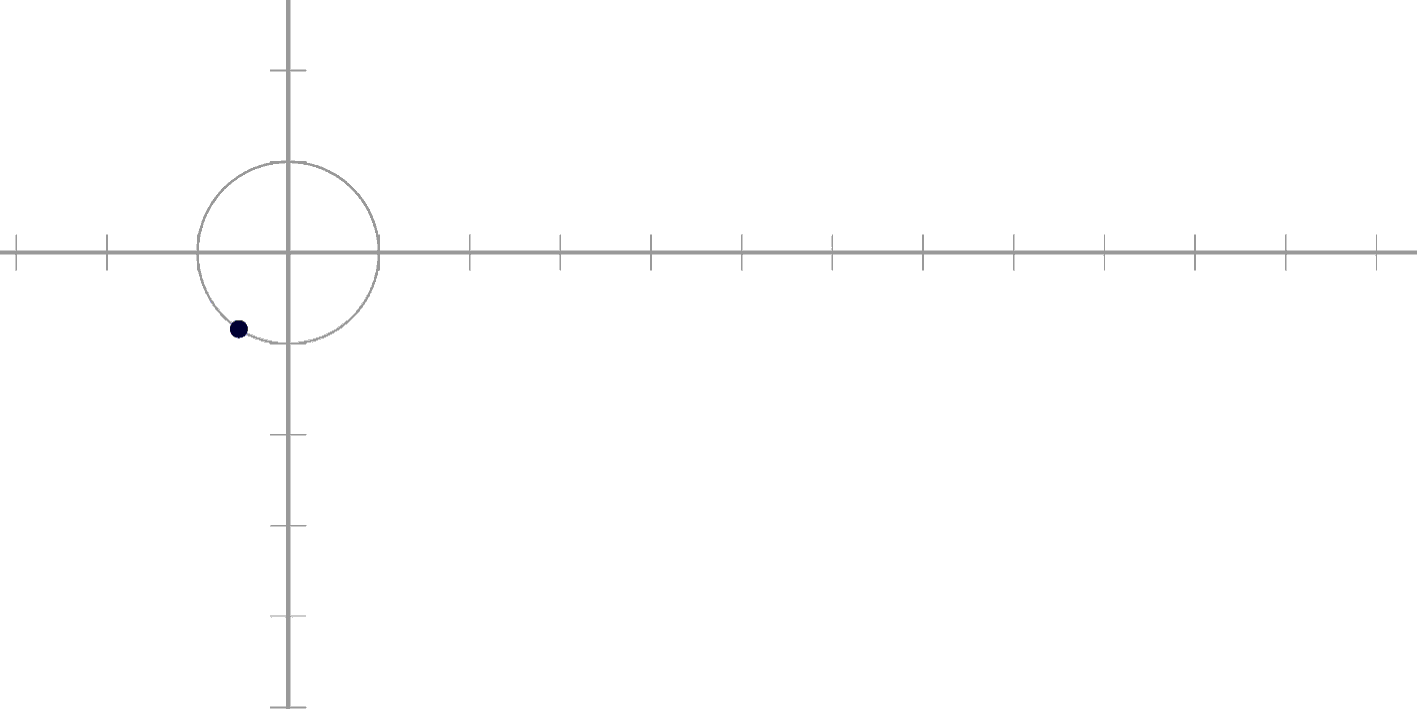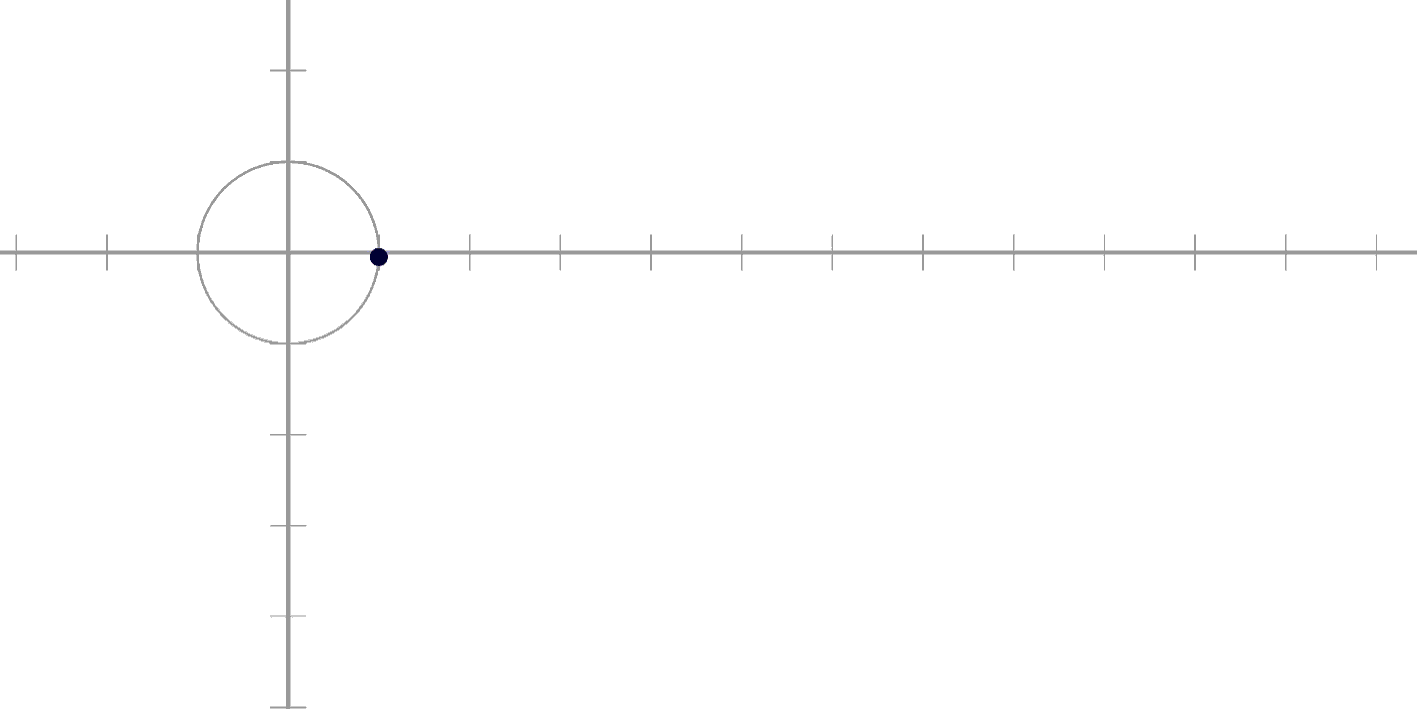
동그라미입니다!
0도부터 360도까지
집어주면 돌아가는 녀석이죠!
이 녀석을 그리는 것이
목표입니다!
그런데 왜 삼각함수?
라고 생각하실 수 있으니까!
선을 좀 그어드릴게요!

선을 그어보았습니다!
자세히 보시면 삼각형이
두 개가 생긴 걸 볼 수 있죠!
둘 다 직각삼각형인 걸
확인하실 수 있습니다~
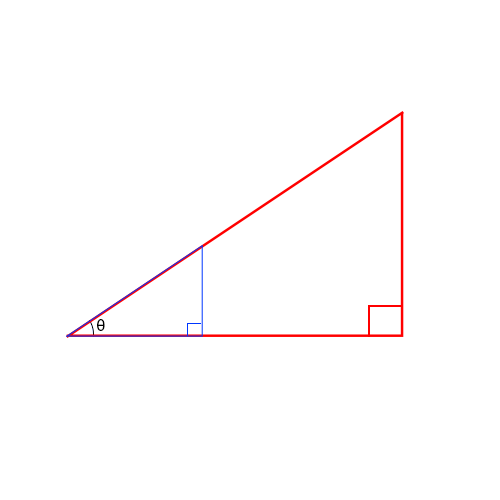
그러면 원이라고 하는 녀석에 있는
저 삼각형들은 아무튼 각도를 정해주면
크기가 어떻게 되었든 상관없이!
"비율"은 항상 똑같습니다!
위에 두 삼각형도 그냥
파란 삼각형을 복사해서
크기만 늘린 거예요! ㅎㅎ

그래서 그 각도에 따라
비율은 항상 정해져 있으니!
그중에서도
높이 / 빗변을
사인(Sin)
이라고 하고
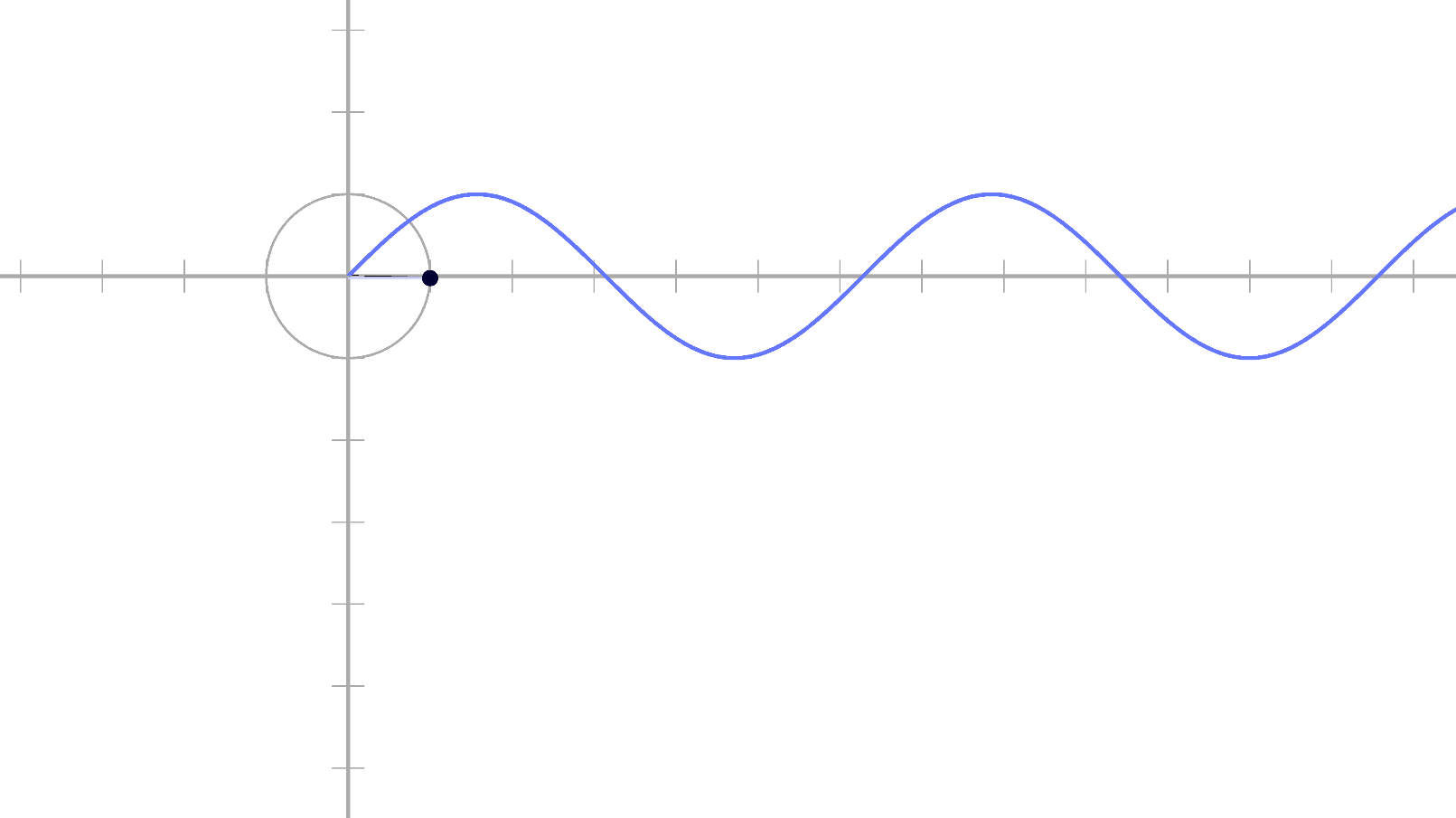
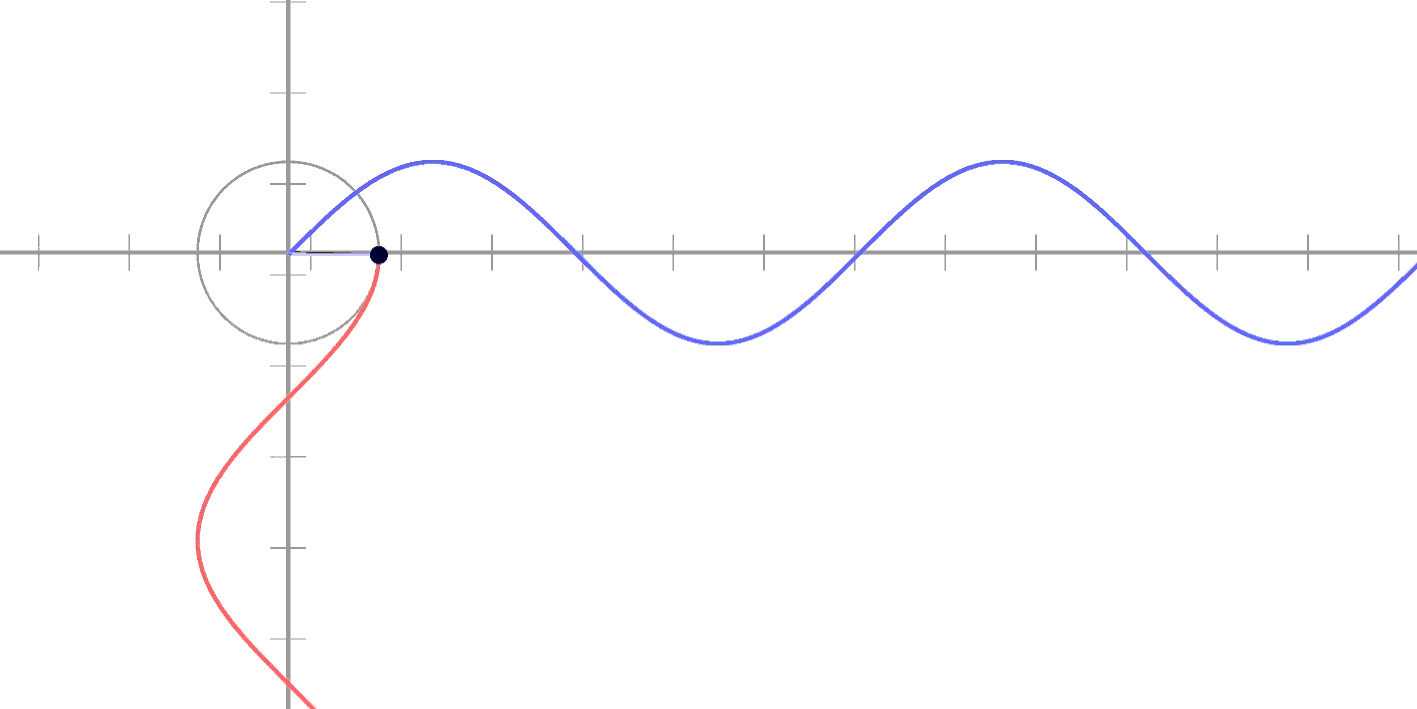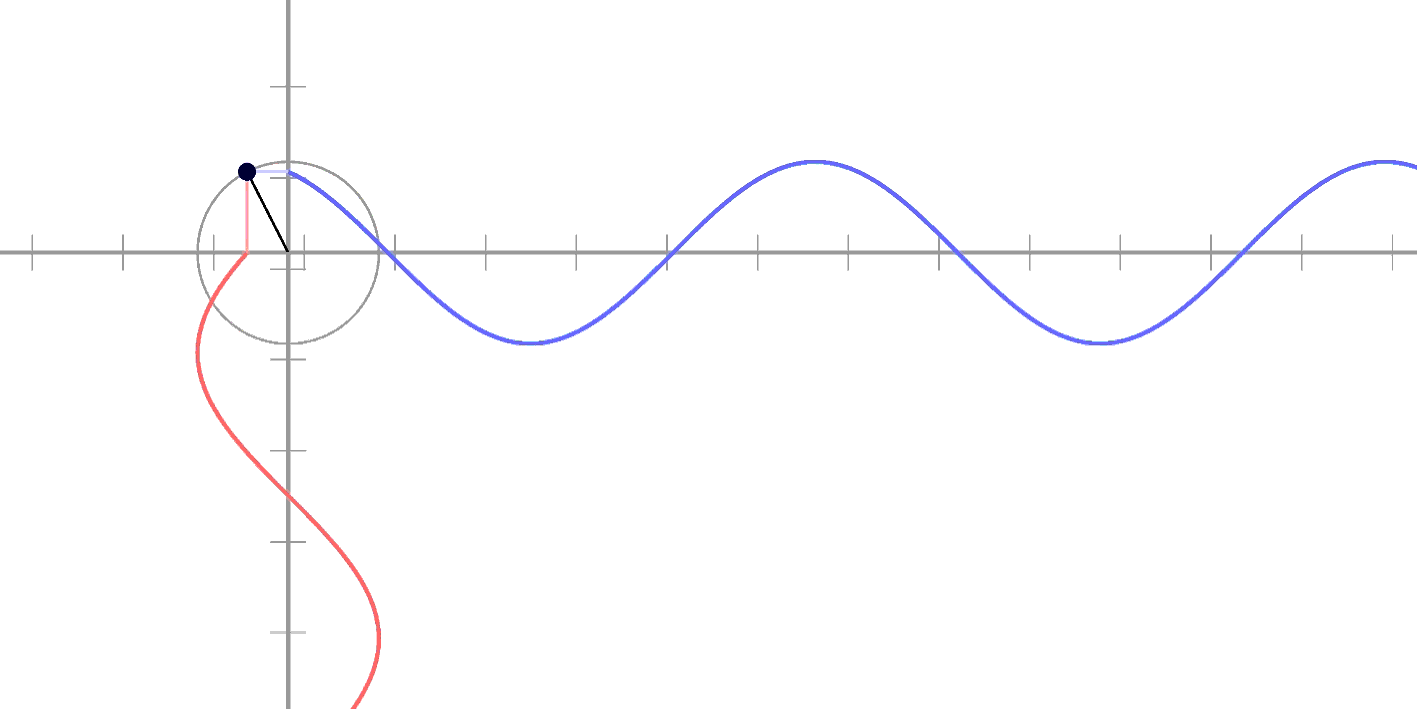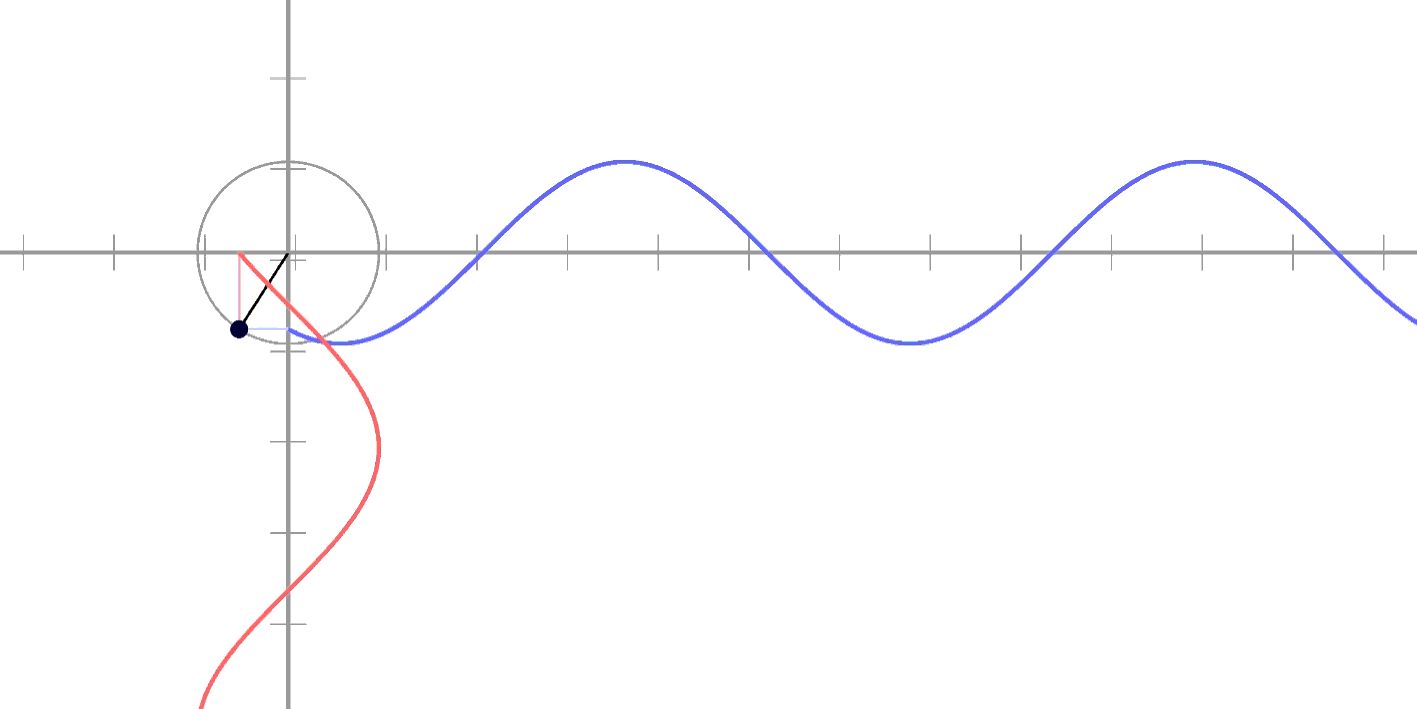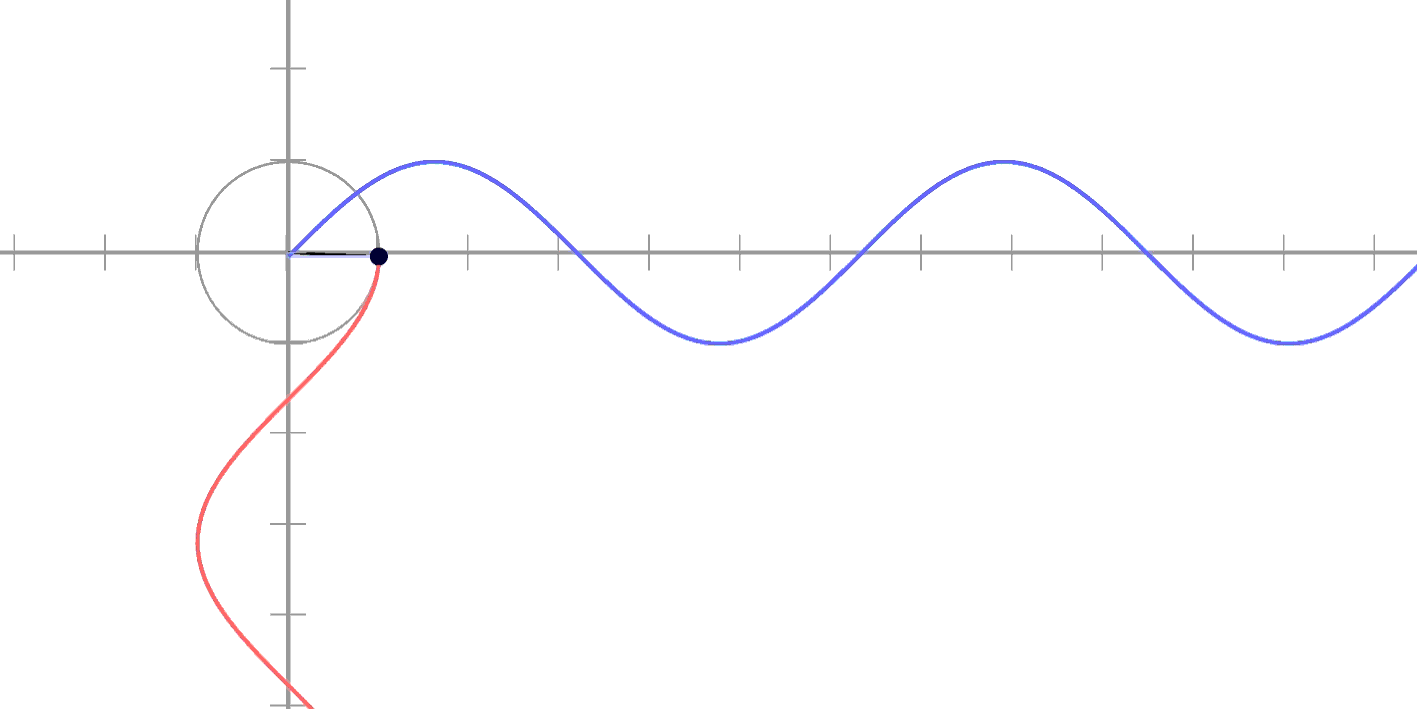
각도에 따라 쭉 따라서
그리면 이렇게 됩니다!
실제로 반복된다는 느낌이죠?
이것은 0 ~ 2π 사이를
반복합니다!
(2π * 반지름) 이 둘레니까!
반지름이 1인 원의
둘레를 나타내고
원의 둘레를 모두 돌았다면
다시 처음부터인 것이죠~
이런 값을 라디안이라고 합니다!
앞으로 자주 사용할 거예요!
..반복되는데
어쩌라는 거죠?
그래서 이걸
눈으로 보여드리기 위해
돌려보겠습니다!
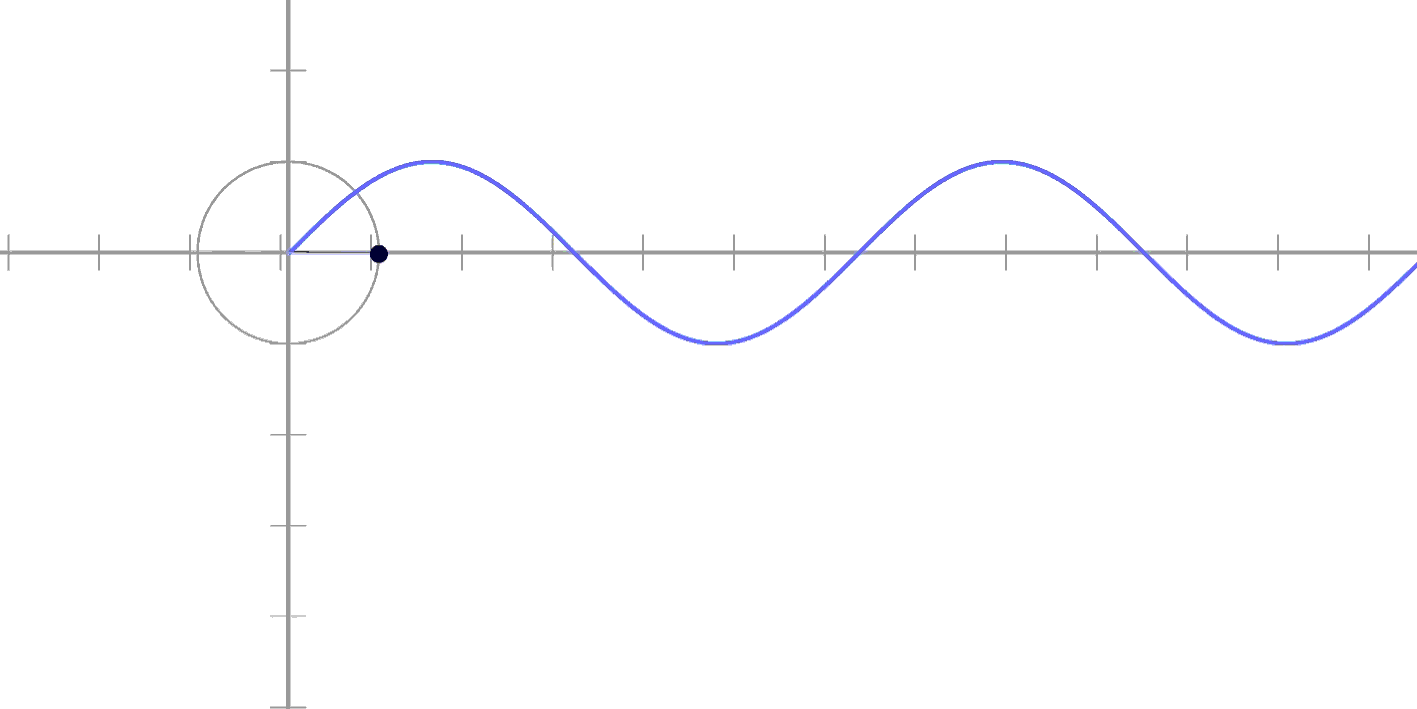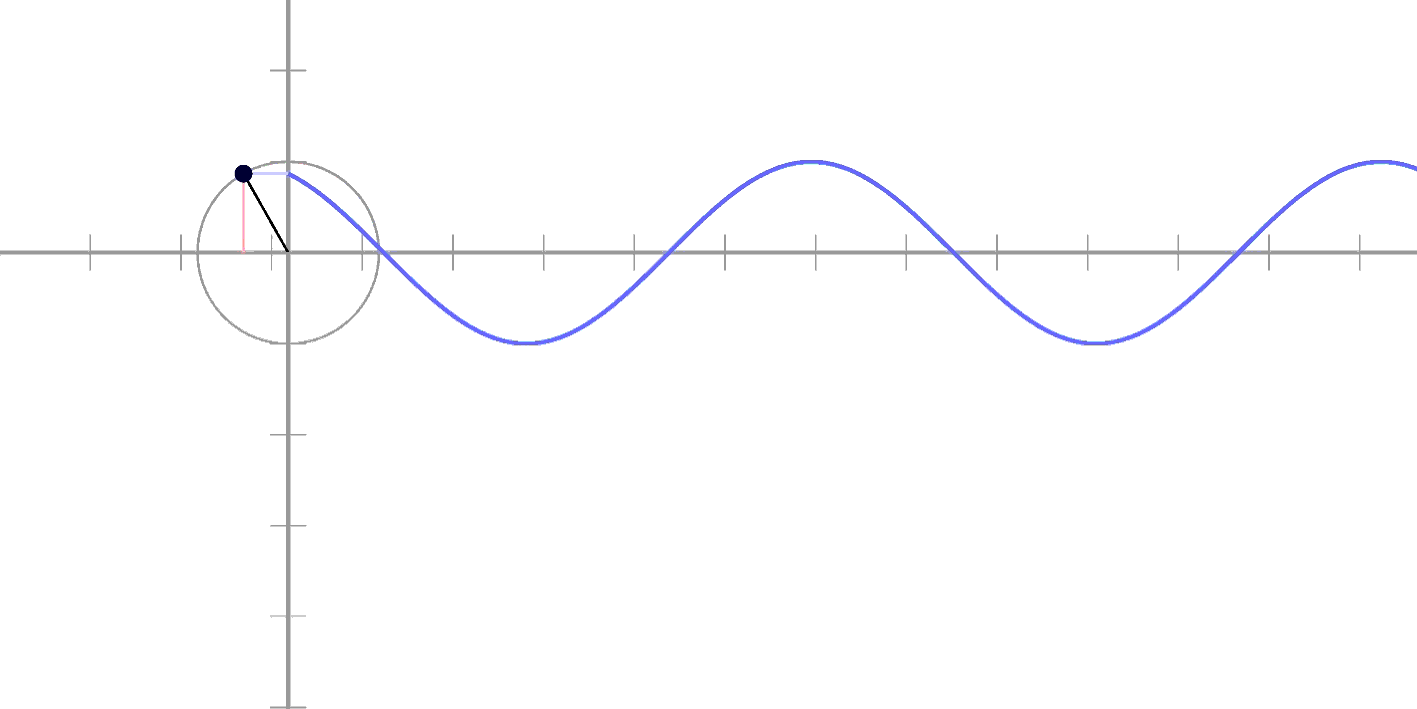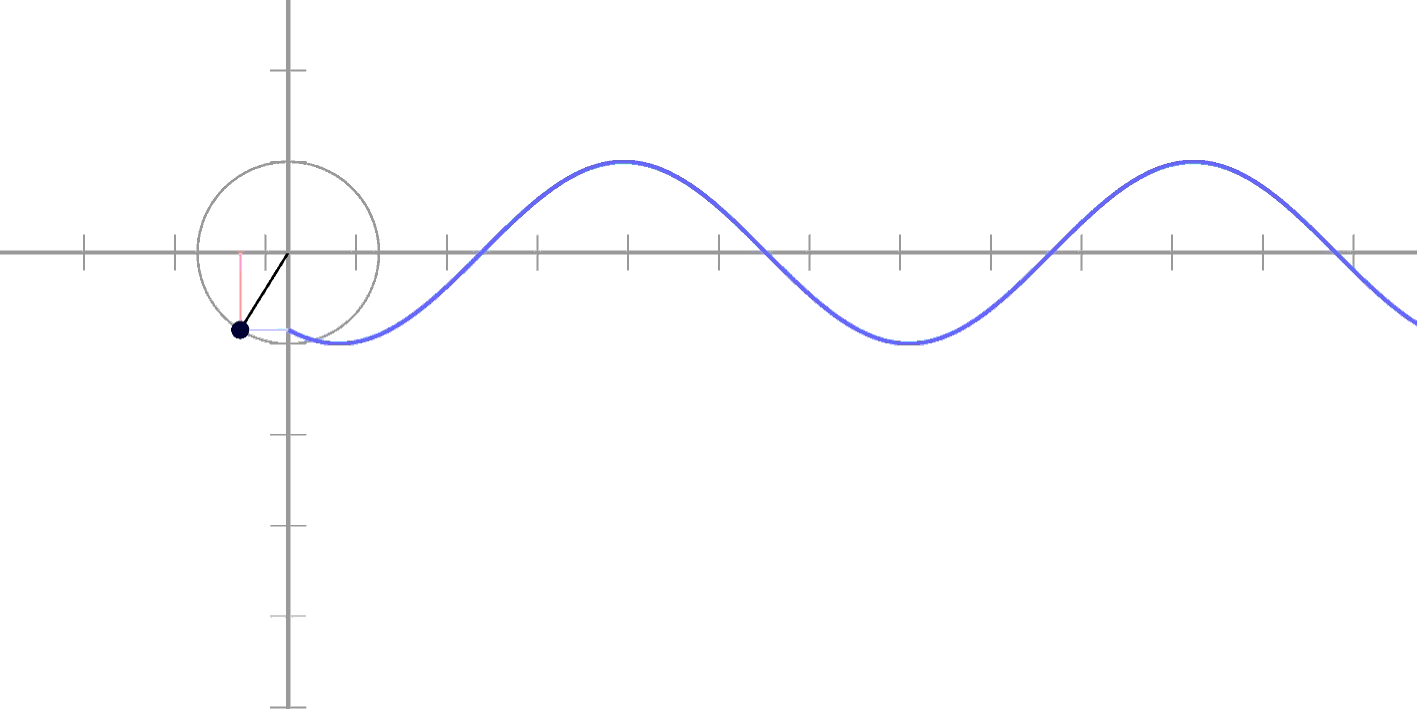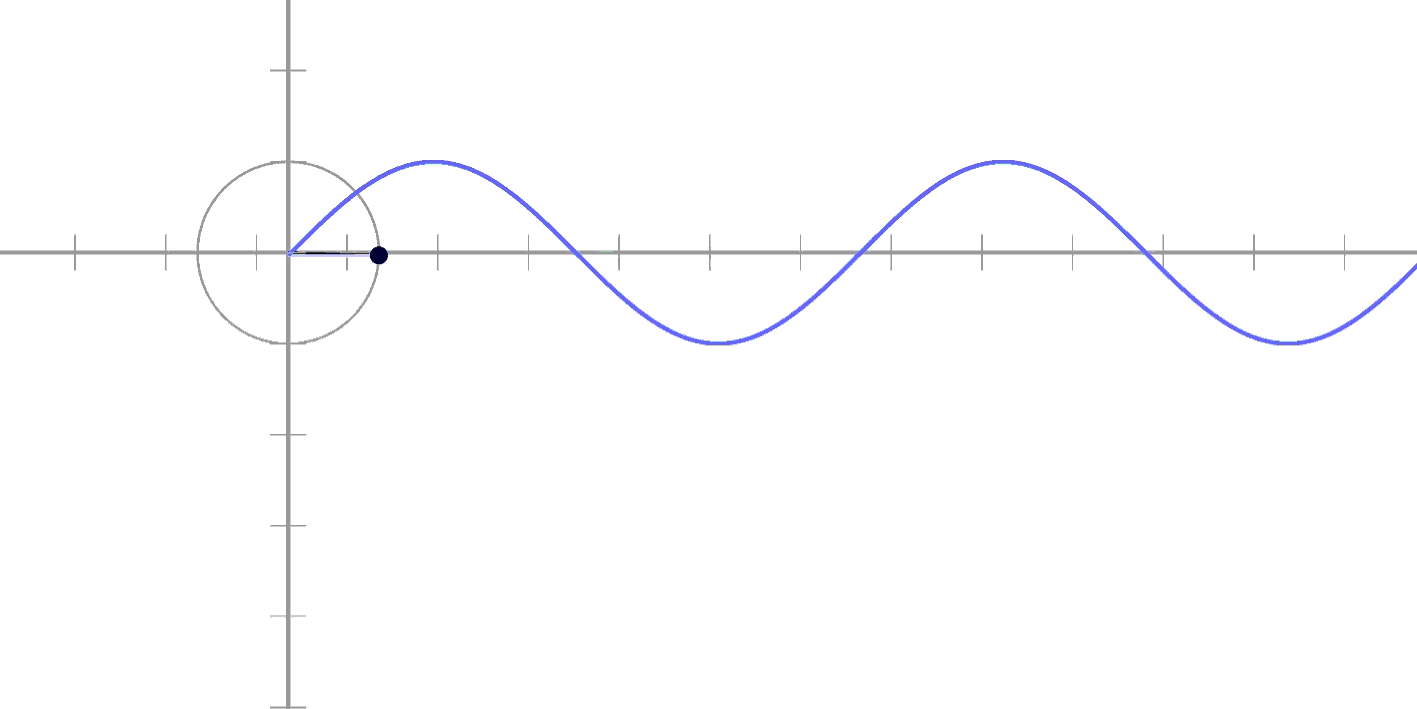
이러면 좀 감이 오시나요?
시간에 따라 움직이다 보면
원의 "높이"와 똑같이
움직이고 있다는 것을
확인하실 수 있죠!
요겁니다 ㅎㅎ
좋아요! 내친김에 하나 더 하죠!

두 번째 그래프!
어.. 근데 아까랑 비슷해 보이네요?
요거는 조금 다른
코사인(Cos)
입니다!
물론 주기나 모양은 같지만!
시작을 1로 합니다!

얘는 높이가 아니라
너비를 말하는 거거든요!
그래서 1로 시작하면 뭐가 되느냐?

x축에다가 연결해봅니다!
느낌 오시나요?
돌립니다!
Sin은 0부터
Cos은 1부터
라고 하는 중요한 차이점으로
각각 원의 y와 x를
표현할 수 있게 되는 거예요!
x = Cos( 값 )
y = Sin( 값 )
이런 느낌이 되는 것이죠!
값은 아까 말해드린 대로
0 ~ 2π
이구요!
| 라디안 | 각도 |
| 0 | 0 |
| 0.25π | 45 |
| 0.5π | 90 |
| 0.75π | 135 |
| 1π | 180 |
| 1.25π | 225 |
| 1.5π | 270 |
| 1.75π | 315 |
| 2π | 360 |
따져보면 이런 느낌입니다!
각도를 직접 쓰시고 싶으시면
각도 / 180 * π
(각도 * 0.0174533)
이렇게 쓰셔도 되구요!
반대로 라디안을 각도로
바꾸고 싶으시면
라디안 * 180 / π
(라디안 * 57.2958)
반대로 이렇게도 되겠죠!
그래서 가장 기본적인
삼각함수로 원을 그리는
방법에 대해서 확인했습니다!
Cos과 Sin의 특징만 알면
되는 문제였네요!
좋습니다! 저희는 그럼 다음 장에선
이걸 가지고 3차원으로 가보도록 할게요!
다음 시간은
삼각함수로 구 그리기
입니다!